平均分散最適化は、異なる資産を組み合わせて最適なポートフォリオを構築する方法を提供します。今回は、この平均分散最適化の解説を行い、最後にpythonで実際に計算してみようと思います。
Contents
平均分散最適化について
基本概念
平均分散最適化で使われる基本的な概念の解説を挟みます。
| 用語 | 説明 |
|---|---|
| リターン (Return) | 投資によって得られる利益のこと。 |
| リスク (Risk) | リターンのブレの大きさを示し、リターンの標準偏差が使われる。 |
| ポートフォリオ (Portfolio) | 複数の投資の組み合わせ。 |
| 分散投資 | リスクを減らすために、異なる資産に投資を分散すること。これは、特定の投資の失敗が全体に与える影響を抑えるためです。 |
| 効率的フロンティア (Efficient Frontier) | リスクとリターンの最適な組み合わせを示す曲線。この曲線上にあるポートフォリオは、同じリスクレベルで最高のリターンを提供します。 |
| 共分散 (Covariance) | 2つの資産のリターンがどの程度連動するかを示す指標。共分散が低い資産を組み合わせることで、ポートフォリオ全体のリスクを低減できます。 |
平均分散最適化の概要
平均分散最適化は、ハリー・マーコビッツによって提唱された投資理論で、複数の資産のリスクとリターンを計算し、それらをどのように組み合わせると最も効率的かを導き出します。
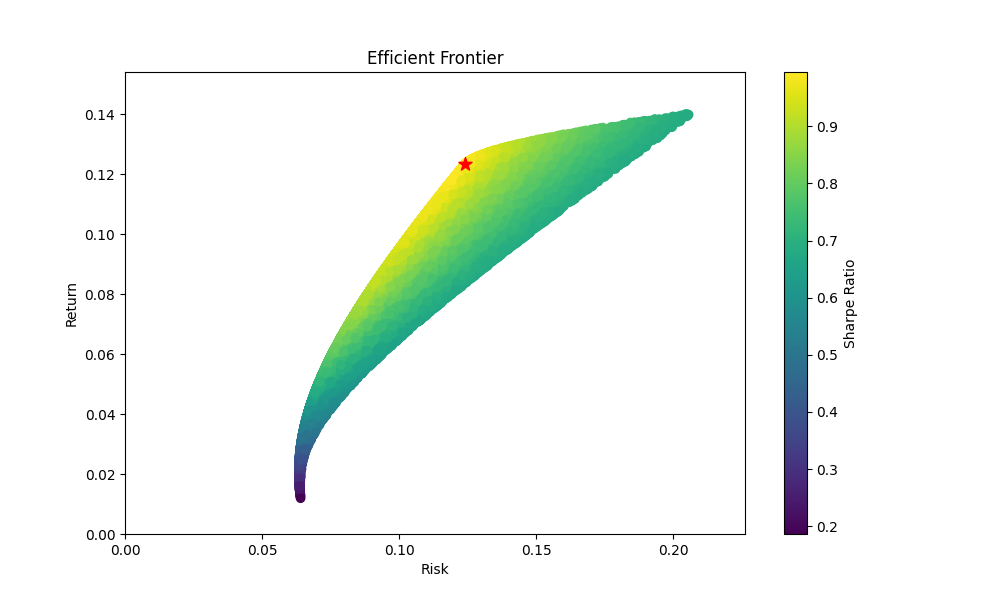
同じリスクレベルで最高のリターンを提供するポートフォリオの組み合わせを示す曲線のことを、この理論の中では効率的フロンティアと呼称しており、この曲線上にあるポートフォリオを買うのが良いとしています。例えば下の図はあるポートフォリオがとりうるリスク/リターンの値をプロットしたものですが、この範囲の中でも上部の境目にある曲線が効率的フロンティアとなります。
そして効率的フロンティアの中でも、原点からの直線に接する点(下の図でいえば星の部分)はシャープレシオが最大になるため、最も効率の良いポートフォリオと言われています。
平均分散最適化のプロセス
以下のような流れで計算します
- 各資産の期待リターンを計算
- 各資産のリスク(分散)を計算
- 資産間の共分散を計算。
- 1~3で計算した情報を元に効率的フロンティアを導出
期待リターンの計算
期待リターンを考える方法はCAPM(その他ファクターモデル)、機械学習など色々考えられますが、そこは今回の本質ではないので、過去のリターンから平均を取る簡単な方法で説明します。ここでは時期によるスケールの違いを考慮するため対数リターンを使用します。
\[\frac{1}{n} \sum_{i=1}^{n} \log(1 + r_i)\]
例えば、過去5年間のリターンが5%、7%、10%、3%、6%だった場合、期待リターンは以下のように計算します。(簡単のため年次で計算)
\[\frac{1}{5} \left( \log(1.05) + \log(1.07) + \log(1.10) + \log(1.03) + \log(1.06) \right) \approx 0.0599\]
リスク(分散)の計算
リターンの標準偏差を計算します。標準偏差は、リターンが平均からどの程度離れているかを示す指標です。
標準偏差の計算方法は以下の通りです:
\[
\sigma^{2} = \frac{1}{N} \sum_{i=1}^{N} (R_{i} – \mu)^{2}
\]
\[
\begin{align}
&\sigma^{2}: \text{分散} \\
&\sigma: \text{標準偏差} \\
&N: \text{リターンの数} \\
&R_i: \text{各期間のリターン} \\
&\mu: \text{平均リターン} \\
\end{align}\\
\]
共分散の計算
共分散を計算するための一般的な式は次の通りです。
\[\text{Cov}(X, Y) = \frac{1}{N} \sum_{i=1}^{N} (X_i – \mu_X)(Y_i – \mu_Y)\]
\[
\begin{align}
& \text{Cov}(X, Y) : \text{資産}X \text{と} Y \text{の共分散} \\
& N : \text{観測数} \\
& X_i, Y_i : \text{各期間の資産} X \text{と} Y \text{のリターン} \\
& \mu_X, \mu_Y : \text{資産} X \text{と} Y \text{の平均リターン} \\
\end{align}
\]
ちょっと複雑だと思うので、資産A・資産B間の共分散を計算する例を置いておきます。
最初に各期間のリターンを収集します。例えば、資産Aと資産Bの過去5年間のリターンが以下だったとします。
資産A: 5%, 7%, 10%, 3%, 6%
資産B: 8%, 5%, 12%, 4%, 7%
次に各期間のリターンから各資産の平均リターンを計算します。
\[ \mu_A = \frac{5\% + 7\% + 10\% + 3\% + 6\%}{5} = 6.2%\]
\[\mu_B = \frac{8\% + 5\% + 12\% + 4\% + 7\%}{5} = 7.2%\]
各リターンと平均リターンの差を計算し、それらの積を求めます。
\[
\begin{align}
&\text{年1:} \quad (5\% – 6.2\%) \times (8\% – 7.2\%) = (-1.2\%) \times 0.8\% = -0.0096\%\\
&\text{年2:} \quad (7\% – 6.2\%) \times (5\% – 7.2\%) = 0.8\% \times (-2.2\%) = -0.0176\%\\
&\text{年3:} \quad (10\% – 6.2\%) \times (12\% – 7.2\%) = 3.8\% \times 4.8\% = 0.1824\%\\
&\text{年4:} \quad (3\% – 6.2\%) \times (4\% – 7.2\%) = (-3.2\%) \times (-3.2\%) = 0.1024\%\\
&\text{年5:} \quad (6\% – 6.2\%) \times (7\% – 7.2\%) = (-0.2\%) \times (-0.2\%) = 0.0004\%\\
\end{align}
\]
最後にこれらの積の平均を求めます(共分散)
\[\text{Cov}(A, B) = \frac{-0.0096\% + (-0.0176\%) + 0.1824\% + 0.1024\% + 0.0004\%}{5} = 0.0516\%\]
これで、資産AB間の共分散が約0.0516%であることがわかります。この値が正であるため、資産Aと資産Bは同じ方向に動く傾向があることを示しています。
効率的フロンティアの構築
今回はモンテカルロ法を用いた簡易的な方法を示します。
効率的フロンティアを構築するためには、ここまでで計算した各資産のリターンとリスク(分散)、共分散行列を用います。以下のステップで効率的フロンティアを構築します:
まず、ポートフォリオの期待リターンを計算します
\[
E(R_p) = \sum_{i=1}^{n} w_i E(R_i)
\]
\[
\begin{align}
&E(R_p) : \text{ポートフォリオの期待リターン} \\
&w_i: \text{資産}i\text{のウェイト} \\
&E(R_i): \text{資産}i\text{の期待リターン} \\
\end{align}
\]
次にポートフォリオの分散を計算します
\[\sigma_p^{2} = \sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}\]
\[
\begin{align}
&\sigma_p^{2} : \text{ポートフォリオの分散}\\
& \sigma_p: \text{ポートフォリオの標準偏差} \\
&w_i, w_j : \text{資産iとjのウェイト} \\
&\sigma_{ij}: \text{資産iとjの共分散} \\
\end{align}
\]
ポートフォリオの標準偏差(x)とリターン(y)をグラフにプロットします。
そしてグラフにプロットする作業を様々なポートフォリオ比率で繰り返すことにより、グラフにポートフォリオがとりうる値(リスク、リターン)の範囲が浮かび上がります(下の図)。そして上側の境目が各リスクレベルで最もリターンの高い(効率の良い)ポートフォリオ、つまり効率的フロンティアと呼ばれています。
※ モンテカルロ法なので試行回数が必要ですが、直観的に効率的フロンティアを描くことができるため、ここでは採用しています。

pythonで実際に計算してみる
VTI、BND、GLDMのETFのみで構成された簡単なポートフォリオで計算してみます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import yfinance as yf
def plot_risk_and_returns(annual_returns, annual_risk):
# Summarize the results
summary = pd.DataFrame({
'Annual Return (%)': annual_returns,
'Annual Risk (%)': annual_risk
})
# Plotting the results
plt.figure(figsize=(10, 6))
plt.scatter(summary['Annual Risk (%)'], summary['Annual Return (%)'], color='blue')
for i, txt in enumerate(summary.index):
plt.annotate(txt, (summary['Annual Risk (%)'][i], summary['Annual Return (%)'][i]), fontsize=12)
plt.title('Annual Return vs. Annual Risk')
plt.xlabel('Annual Risk (%)')
plt.ylabel('Annual Return (%)')
plt.grid(True)
plt.xlim(0, summary['Annual Risk (%)'].max() * 1.1) # Extend x-axis slightly
plt.ylim(0, summary['Annual Return (%)'].max() * 1.1) # Extend y-axis slightly
plt.savefig("risk_and_returns.png")
def plot_cov_matrix(cov_matrix):
# Display the covariance matrix as a heatmap
plt.figure(figsize=(10, 8))
sns.heatmap(cov_matrix, annot=True, fmt=".6f", cmap='coolwarm', linewidths=.5)
plt.title('Covariance Matrix Heatmap')
plt.savefig("cov_matrix.png")
# Define the tickers
tickers = ['VTI', 'BND','GLDM']
# Fetch historical data for the past 10 years
data = yf.download(tickers, start='2014-05-31', end='2024-05-31')['Adj Close']
log_returns = np.log(data / data.shift(1)).dropna()
# Calculate annual log returns and risk
annual_log_returns = log_returns.mean() * 252
annual_risk = log_returns.std() * np.sqrt(252)
plot_risk_and_returns(annual_log_returns, annual_risk)
# Calculate covariance matrix
cov_matrix = log_returns.cov() * 252
plot_cov_matrix(cov_matrix)
# Monte Carlo simulation
num_portfolios = 100000
results = np.zeros((3 + len(tickers), num_portfolios))
for i in range(num_portfolios):
weights = np.random.random(len(tickers))
weights /= np.sum(weights)
portfolio_return = np.dot(weights, annual_log_returns)
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
results[0, i] = portfolio_return
results[1, i] = portfolio_risk
results[2, i] = portfolio_return / portfolio_risk
for j in range(len(tickers)):
results[3 + j, i] = weights[j]
# Create DataFrame
columns = ['Return', 'Risk', 'Sharpe Ratio'] + tickers
results_frame = pd.DataFrame(results.T, columns=columns)
# Find the portfolio with the maximum Sharpe Ratio
max_sharpe_idx = results_frame['Sharpe Ratio'].idxmax()
max_sharpe_portfolio = results_frame.loc[max_sharpe_idx]
# Plot efficient frontier
plt.figure(figsize=(10, 6))
plt.scatter(results_frame['Risk'], results_frame['Return'], c=results_frame['Sharpe Ratio'], cmap='viridis')
plt.colorbar(label='Sharpe Ratio')
plt.xlabel('Risk')
plt.ylabel('Return')
plt.title('Efficient Frontier')
plt.scatter(max_sharpe_portfolio['Risk'], max_sharpe_portfolio['Return'], color='red', marker='*', s=100) # Max Sharpe Ratio point
plt.xlim(0, results_frame['Risk'].max() * 1.1) # Extend x-axis slightly
plt.ylim(0, results_frame['Return'].max() * 1.1) # Extend y-axis slightly
plt.savefig("mvo.png")
# Output the portfolio with the maximum Sharpe Ratio
max_sharpe_weights = max_sharpe_portfolio[tickers]
print(f"Max Sharpe Ratio Portfolio Weights:n{max_sharpe_weights}")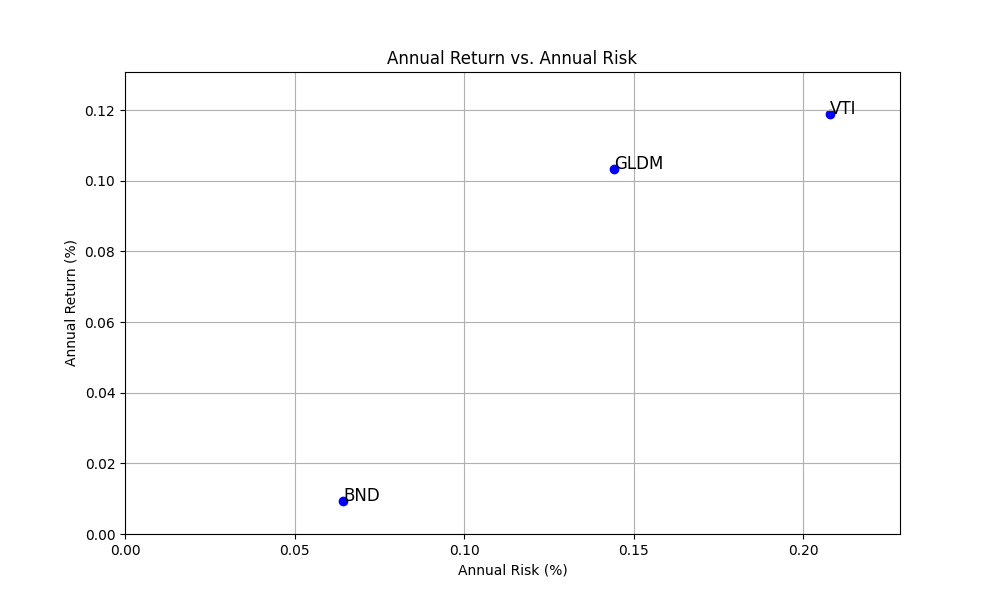
以下が算出された共分散行列です。対角成分が分散、それ以外が共分散を示します。
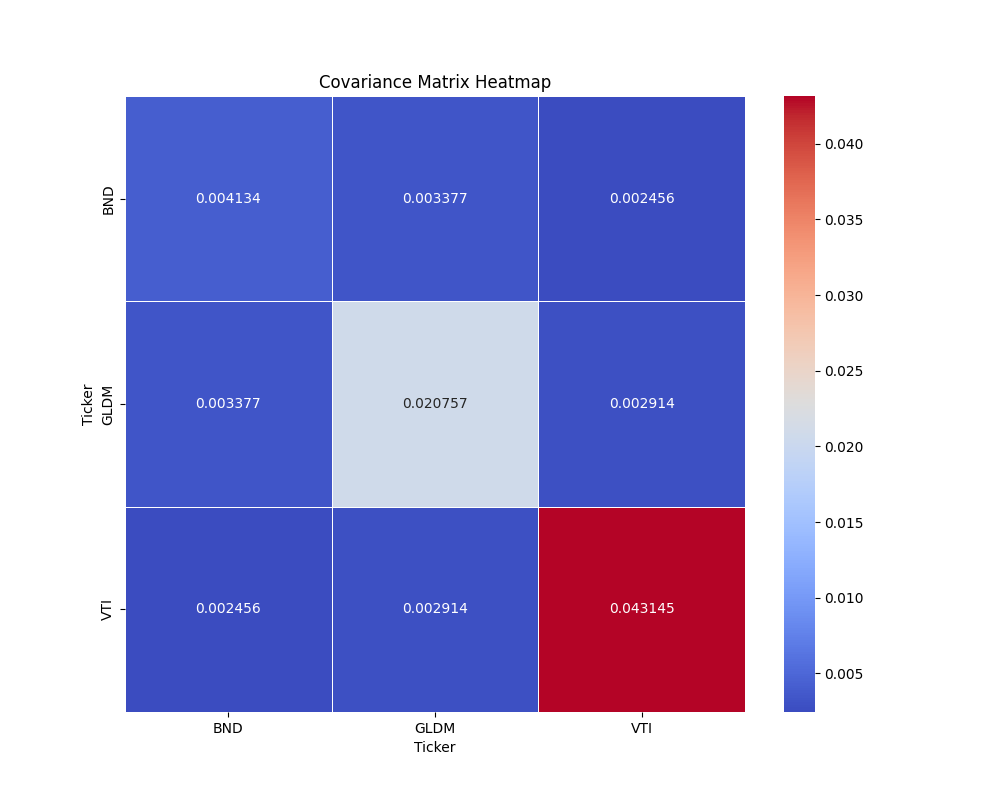
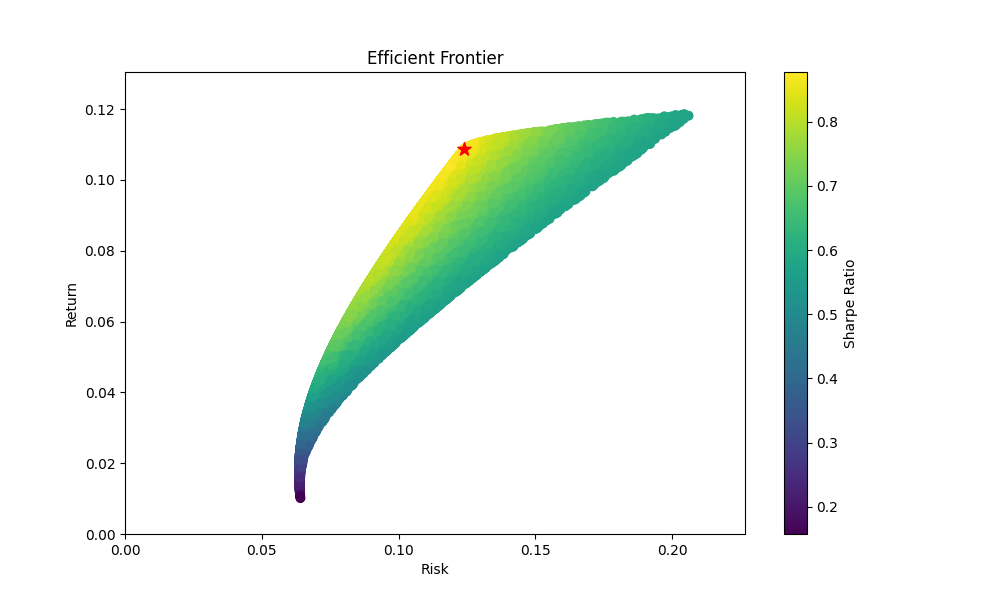
そして、下の図が効率的フロンティアをモンテカルロ法で図にしたものになります。
最後に
異なる資産を組み合わせて最適なポートフォリオを構築する平均分散最適化という手法を紹介しました。
今回は説明と自分の理解のため、簡単な方法で計算を行いましたが、最適化問題として解けばより効率的に導出できるので、次はその方法も触れようと思います。
※触れました
ポートフォリオ構築に関連する他のモデルを知りたい方は下記のリンク集をぜひご活用ください。